Symbolic Algebra Basics

Symbolic algebra serves as a tool to calculate A.C. phenomena.
Invented by Charles P. Steinmetz.

Definition

a + jb = E = 1

Where:

• ± a, cos θ, the active/power factor (% horizontal component, x-axis)
• ± b, sin θ, the reactive/induction factor (% vertical component, y-axis)
• j is the distinguishing index
• E is a variable that has a active and reactive part (magnetic effect, EMF, in this case)

Rules:

• If a + jb = 0, then a = 0 and b = 0

j what?

The definition of j is as follows, this is the imaginary unit:

j = √ -1

j ^ 0 = + 1
j ^ 1 = + j
j ^ 2 = - 1
j ^ 3 = - j

How to use

What we’re actually doing is combination by the parallelogram law.
We’re looking for the hypothenuse.

a + jb = Math.sqrt(
  Math.pow(a, 2) +
  Math.pow(b, 2)
)

Phase angle

// tan θ = b / a
θ = arctan(b / a)
a + jb = cos θ + sin θ

Coordinate System

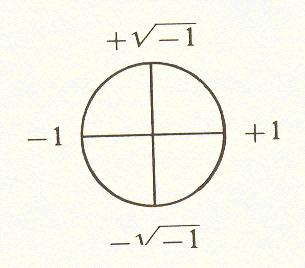
The following uses an example phase angle of 0º,
which means that cos θ will be 1:

(a + jb) * j ^ 0 = a + jb      # (+1, 0)    + 1       no rotation
(a + jb) * j ^ 1 = ja - b      # (0, -1)    - √-1     advance 90º
(a + jb) * j ^ 2 = -a - jb     # (-1, 0)    - 1       reverse, 180º rotation
(a + jb) * j ^ 3 = -ja + b     # (0, +1)    + √-1     advance 270º

Or in different terms:

  a + jb = Math.sqrt(   a ^ 2 + b ^ 2 )
 ja -  b = Math.sqrt(   a ^ 2 - b ^ 2 )
- a - jb = Math.sqrt( - a ^ 2 - b ^ 2 )
-ja +  b = Math.sqrt( - a ^ 2 + b ^ 2 )

This can be altered. For example, you can choose a different starting position, by rotating it, or you could go in the opposite direction. When going in the other direction, a different symbol is usually used, for example, j is forwards and k is backwards.

Operations

Addition

(a + jb) + (c + jd)

# Process
= a + jb + c + jd
= a + c + jb + jd

# Result
= (a + c) + j (b + d)

Subtraction

(a + jb) - (c + jd)

# Process
= a + jb - c - jd
= a - c + jb - jd

# Result
= (a - c) + j (b - d)

Multiplication

(a + jb) * (c + jd)

# Process
= (a * c) + (a * jd) + (jb * c) + (jb * jd)
= ac + ajd + cjb + jbjd
= ac + j * ad + j * cb + j^2 * bd
= ac + j (ad + cb) + j^2 * bd
= (ac + j^2 * bd) + j (ad + bc)

# Use rule defined above: j ^ 2 = - 1
= (ac + (-1 * bd)) + j (ad + bc)
= (ac + (-bd)) + j (ad + bc)

# Result
= (ac - bd) + j (ad + bc)

Division

(a + jb) / (c + jd)

# TODO